| ИЕРОГЛИФ | БИБЛИОТЕКА | |
| http://Hiero.Ru |
|
|
В первой статье речь шла о том, что привычные представления о глубине резкости уже не соответствуют современным параметрам фотоаппаратуры и плёнок. Оказалось, что требования к резкости изображения нужно усилить примерно в семь раз. Правила расчёта глубины резкости легко переформулируются для новых стандартов, но при этом вычисленная глубина резкости становится ничтожно малой. Однако это не согласуется с моей практикой
Фокусировка на более дальние расстояния существенно улучшает разрешимость удаленных объектов; однако и предметы, расположенные ближе ближней границы зоны резкости, похоже, часто отображаются достаточно приемлемо. В данной статье я рассмотрю именно это явление. Оно не всегда имеет место, однако, его возможно предсказать и использовать.
Но прежде позвольте мне исправить две ошибки в предыдущей статье. Первую ошибку заметили многие читатели. Рис. 2, показывающий шкалу глубин резкости для объектива 50/8, установленного на гиперфокальное расстояние, неправилен. Дабы уместить диаграмму в полосу журнала, верстальщик разрезал её на две и сместил шкалы друг относительно друга! Рис. 1 в данной статье показывает, как на самом деле должна была выглядеть та диаграмма.
 Рис. 1: Шкала глубины резкости для 50-мм объектива, сфокусированного на гиперфокальное расстояние для диафрагмы f/8. Шкала диафрагм размечена вплоть до значения f/1. Предполагается кружок нерезкости 1/30 мм. |
Вторая ошибка связана с моей собственной невнимательностью. Я заявил, что для моего 200 мм Micro-Nikkor с диафрагмой f/5,6, сфокусированного на бесконечности, табличная зона резкости начинается в 1929,22 метрах. Я и в самом деле нашёл это число в таблице (в книге по объективам Nikkor), только таблица эта относилась к фокусному расстоянию в 600 мм, а не в 200 мм! Правильное значение для 200-мм объектива - 215 метров.
И тем не менее, факт остаётся фактом: вычисление глубины резкости с тремя значащими цифрами (не говоря уже о шести) - совершенно бессмысленное занятие (если только вы не занимаетесь макросъёмкой).
Но вернёмся к нашей основной теме. Я заявил в прошлой статье, что наша прекрасная модель, находящаяся в 1929,22 (ну, или в 215) метрах от нас, может подойти значительно ближе к камере, и мы всё равно не увидим особенных изменений в её изображении - в видоискателе или на отпечатке. Объектив, сфокусированный на бесконечности, обладает уникальными свойствами. Он строит одинаково детализированное изображение предмета, независимо от того, насколько этот предмет удалён. Наша модель могла бы подойти прямо к камере, и мы всё равно видели бы её в видоискателе с той же степенью детализации, как если бы она была в тридцати футах, в сотне футах или в семистах футах от нас. Правда, на больших расстояниях начинают сказываться дифракционные эффекты, которые слегка портят изображение.
Традиционные методы расчёта глубины резкости отталкиваются от резкости изображения на плёнке. С точки зрения изображения на плёнке, объектив, наведённый на бесконечность, даёт тем более резкое, детализированное, изображение, чем дальше объект от камеры. С точки же зрения объекта ситуация иная. Если мы можем различить зрачок глаза нашей модели, когда она в 20 футах от нас, то мы также сможем его различить и в сотне и (вероятно) в семи сотнях футов. Точно так же мы увидим её зрачок и в десяти, и в пяти футах. Её глаз может заполнить весь кадр, но мы всё равно будем различать зрачок. Изображение при этом, конечно, не будет столь резким, каким могло бы быть (если бы мы могли перефокусироваться), но будет всё же достаточно четким, чтобы мы продолжали различать те же детали, которые мы различали на более далёком расстоянии.
Итак, как мы можем определить, какое разрешение в пространстве объектов обеспечит нам данный объектив? Какие детали, какие черты лица модели, какого размера камни на земле мы сможем различить? Для объектива, наведённого на бесконечность, ответ предельно прост. Посмотрите на объектив спереди, и закройте диафрагму до того значения, которое собираетесь использовать. Тот размер отверстия, который вы увидите - это и есть минимальный размер деталей, разрешаемых этим объективом при наведении его на бесконечность. Если рабочее отверстие - около трёх миллиметров, то мы сможем различить зрачок глаза. Если отверстие больше, например, 25 мм, то мы сможем увидеть, что у человека два глаза, но и только.
Как было сказано выше, дифракционные эффекты также ограничивают разрешение. Я не буду сейчас углубляться в детали, а просто приведу пример. Пусть у нас есть объектив 50 мм с диафрагмой f/10 (т. е. с 5-миллиметровым отверстием). Тогда самый маленький объект, который нам позволят увидеть дифракционные эффекты, будет иметь размер порядка 1/8000 дистанции от камеры до объекта. Т. е. в 8000 футах (примерно 2,5 км) объектив 50/10 сможет различить объекты размером не менее одного фута. Можно сказать и иначе: на расстояниях до 160 футов (40 метров), разрешение будет ограничено действующим отверстием линзы (5 мм). На больших дистанциях дифракционные эффекты начинают ограничивать разрешение значением 1/8000 расстояния от камеры до объекта. Всё вышесказанное, конечно, относится к объективу, сфокусированному на бесконечность.
Важно понять, что все объективы, имеющие одно и то же рабочее отверстие, "видят мир" примерно одинаково, независимо от их фокусных расстояний. Чтобы проиллюстрировать этот эффект, я сделал несколько снимков тремя разными объективами, установив у них одинаковые действующие отверстия и сфокусировав их на бесконечности. Этими объективами были: 24 мм (f/4), 50 мм (f/8) и 100 мм (f/16). Действующее отверстие у всех них было 4,5 мм. Рис. 2 демонстрирует некоторые результаты этого эксперимента. Таблички с числам, которые держит модель, показывают фокусное расстояние и дистанцию съёмки. Дистанция выбиралась так, чтобы все снимки имели одинаковый масштаб. Я думаю, вы согласитесь с тем, что, кроме некоторого снижения контраста с увеличением фокусного расстояния, все три снимка очень похожи. Точка на щеке модели - это чёрный бумажный кружок 8 мм в диаметре, приклеенный специально для оценки резкости.
 Рис. 2: Три портрета Джун, сделанные тремя разными объективами: 24 мм, 50 мм и 100 мм, сфокусированными на бесконечности. Действующее отверстие во всех трёх случаях - 6 мм. Результаты практически одинаковы! |
Когда объектив наведён на бесконечность, он видит мир как бы нарисованным кистью, причём размер кисти - это размер действующего отверстия объектива. Чем больше отверстие - тем кисть грубее, чем оно меньше - тем кисть тоньше. На рис. 3 я изобразил ход лучей в объективе. Сплошные линии показывают лучи, приходящие от маленького, бесконечно удалённого источника света. Эти лучи собираются в крошечную яркую точку на плёнке. Точечный объект, находящийся ближе к камере, на расстоянии D, будет сфокусирован за плёнкой, как показано пунктирной линией. Его изображение на плёнке будет не точкой, а кругом. Это - то, что называется кружком нерезкости. Если мы измерим его размер, а потом вычислим, каким был бы объект на расстоянии D, если бы этот кружок был его резким изображением, то мы получим диаметр линзы (тонкая сплошная линия на рисунке)! И этот размер не зависит от D. Это, конечно, не строгое доказательство, но поверьте, всё так и есть.
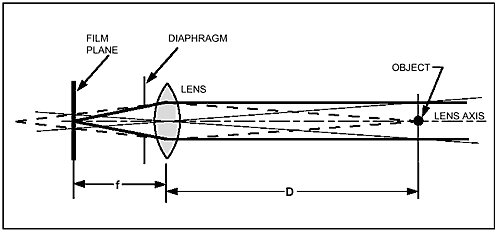 Рис. 3: Ход лучей в объективе, наведённом на бесконечность. Объекты ближе бесконечности фокусируются за плоскостью плёнки. Получающийся на плёнке кружок тем больше, чем больше действующее отверстие объектива. Тонкие линии, проходящие через центр линзы, показывают, что в пространстве предметов этот кружок представляется объектом с диаметром, равным диаметру объектива. |
Более удобной может оказаться следующая метафора. Её предложил Paul Rumsey, читатель Shutterbug-a: "Если рассматривать камеру как слайд-проектор, а объект съёмки - как экран, то всё становится очевидным!" Действительно, когда объектив наведён на бесконечность, то каждая точка на плёнке образует пучок параллельных лучей, такого же диаметра, как и диаметр объектива. И на каком бы расстоянии не был экран (т.е. объект съёмки), этот пучок нарисует на нём пятно одинакового диаметра.
Таким образом, если некие детали сцены больше, чем диаметр объектива, то они будут различимы на плёнке, если меньше - то они не будут различимы, причём независимо от расстояния.
До того, как я всё это осознал, я обычно фокусировался на гиперфокальном расстоянии, как советуют многие учебники, чтобы "получить максимальную глубину резкости". Но на самом деле, в этом нет особого смысла. Пусть у нас объектив 50 мм и диафрагма f/8 (скажем, из-за условий освещённости). Тогда гиперфокальное расстояние - примерно 32 фута, и ближняя граница зоны резкости - 16 футов. Предположим, наша сцена простирается от трёх футов и до бесконечности. Для объектов в трёх футов, 32 фута - это всё равно, что бесконечность. Изменение фокусировки с 32 футов до бесконечности на них практически никак не повлияет, однако резкость дальних объектов при этом значительно улучшится. Действующее отверстие нашего объектива - примерно 6 мм, и если размеры объектов на переднем плане - порядка 5-6 мм, то всё в порядке. Если же ближние объекты мельче, и при этом они важны, то выход только один - надо использовать меньшую апертуру. Однако мы договорились использовать f/8. Единственное решение - использовать более короткофокусный объектив. 35-мм объектив позволил бы нам различить объекты размером в 4 мм, 24-миллиметровый улучшил бы разрешение до 3 мм - около 1/8 дюйма. Этого достаточно, чтобы на снимке получилась, скажем, отдельные травинки.
По моему опыту, человеку интересен прежде всего человек. Если мы видим человека в пейзажном снимке и можем узнать его в лицо, мы говорим: "О, какая чёткая картинка!". Если же его образ слишком размыт, чтобы мы могли его идентифицировать, то мы говорим: "Снимок мог быть и почётче". Я обнаружил, что "волшебное значение" резкости - это где-то 3-5 мм. С такой резкостью человек узнаваем. Снятый с апертурой 10 мм, человек выглядит решительно нечётко. На 25 мм мы, вероятно, не смогли бы узнать его. А на 200 мм мы вообще не могли бы быть уверены, что эти размытые пятна - люди.
Вы наверняка читали о том, что Энзел Адамс часто использовал 300-мм объектив, закрытый до f/64? Теперь вы можете сами оценить резкость его пейзажей - апертура составляла всего 5 мм!
Внимание! Все статьи в нашей библиотеке являются авторскими. Копирование на другие сайты, перепечатка или иное использование статей без согласия их авторов запрещено (ссылки на автора или на наш сайт недостаточно — см. статью «Авторские права в цифровую эпоху»).
|
© «Иероглиф» (контакты) © 1998-2026 Давид Мзареулян, Сергей Козинцев Права на все работы, опубликованные на сайте, принадлежат их авторам |
|
||||||||||